מה זה תחומי חפיפה?
ניתן לחלק את בעיות החפיפה לשני סוגים: הסוג הראשון הוא מצב שבו ידועה לנו החפיפה בין הקבוצות.
הסוג השני הוא מצב שבו לא נתונה לנו החפיפה בין הקבוצות.
החפיפה בין הקבוצות נתונה
כאשר החפיפה בין הקבוצות נתונה, יש לסדר את הנתונים בצורה נוחה.
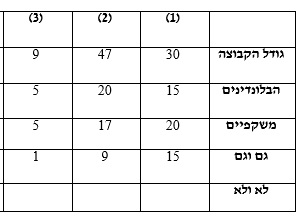
ניקח לדוגמה כיתה בת 40 ילדים. 20 מתלמידי הכיתה אוהבים שוקולד ו- 30 מתלמידי הכיתה אוהבים גלידה.
נתון: 15 מהם אוהבים גם שוקולד וגם גלידה. כמה מתלמידי הכיתה לא אוהבים גלידה וגם לא אוהבים שוקולד?
ניתן לחשוב על השאלה בצורה הבאה: בכיתה נעשתה הצבעה שבה נשאלו התלמידים מי אוהב שוקולד ומי אוהב גלידה.
כאשר נשאלו התלמידים מי אוהב שוקולד, הצביעו 20 מתלמידי הכיתה. כאשר נשאלו מי אוהב גלידה, הצביעו 30 מתלמידי הכיתה.
בסך הכול היו 50 הצבעות, אך נתון ש-15 מתלמידי הכיתה הצביעו פעמיים (גם לשוקולד וגם לגלידה).
לכן נחסר את מספר התלמידים שהצביעו פעמיים (15) מסך ההצבעות (50) כדי לקבל את מספר תלמידי הכיתה שהצביעו לפחות באחת ההצבעות: 35=50-15.
כעת אנו צריכים למצוא את מספר תלמידי הכיתה שלא הצביעו בשתי ההצבעות.
נחסר את מספר התלמידים שהצביעו בלפחות מאחת ההצבעות (35) ממספר תלמידי הכיתה (40): 5=40-35.
כעת אנו צריכים למצוא את מספר תלמידי הכיתה שלא הצביעו בשתי ההצבעות.
נחסר את מספר התלמידים שהצביעו בלפחות מאחת ההצבעות (35) ממספר תלמידי הכיתה (40): 5=40-35.
5 תלמידים בכיתה לא אוהבים שוקולד וגם לא אוהבים גלידה.
ניתן לראות זאת בצורה גרפית:
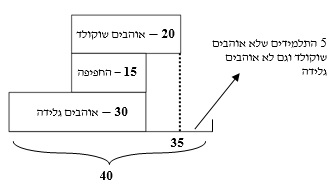 ניתן לראות כי כאשר סידרנו בסרטוט את הקבוצות ואת החפיפה ביניהן, נשאר תחום שבו 5 תלמידים שלא אוהבים שוקולד וגם לא אוהבים גלידה.
ניתן לראות כי כאשר סידרנו בסרטוט את הקבוצות ואת החפיפה ביניהן, נשאר תחום שבו 5 תלמידים שלא אוהבים שוקולד וגם לא אוהבים גלידה.
החפיפה בין הקבוצות לא נתונה
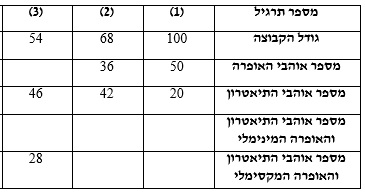
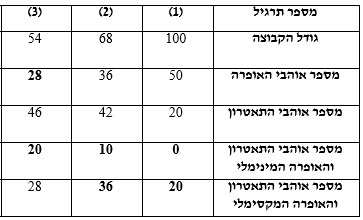
כאשר החפיפה בין הקבוצות לא נתונה לנו, נצטרך למצוא את החפיפה המינימלית ואת החפיפה המקסימלית.
נציג את הדרכים למציאת החפיפה המינימלית ולמציאת החפיפה המקסימלית.
ניתן לראות זאת בצורה גרפית:
 ניתן לראות כי כאשר סידרנו בסרטוט את הקבוצות ואת החפיפה ביניהן, נשאר תחום שבו 5 תלמידים שלא אוהבים שוקולד וגם לא אוהבים גלידה.
ניתן לראות כי כאשר סידרנו בסרטוט את הקבוצות ואת החפיפה ביניהן, נשאר תחום שבו 5 תלמידים שלא אוהבים שוקולד וגם לא אוהבים גלידה.החפיפה בין הקבוצות לא נתונה
כאשר החפיפה בין הקבוצות לא נתונה לנו, נצטרך למצוא את החפיפה המינימלית ואת החפיפה המקסימלית.
נציג את הדרכים למציאת החפיפה המינימלית ולמציאת החפיפה המקסימלית.

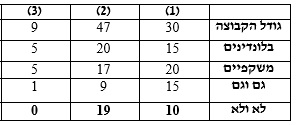
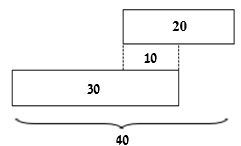 במצב הנתון בסרטוט יש 10 ילדים שאוהבים רק שוקולד ו- 20 ילדים שאוהבים רק גלידה.
במצב הנתון בסרטוט יש 10 ילדים שאוהבים רק שוקולד ו- 20 ילדים שאוהבים רק גלידה. 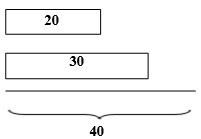 במצב זה יש 10 ילדים שאוהבים רק גלידה ו- 10 ילדים שלא אוהבים גלידה וגם לא אוהבים שוקולד.
במצב זה יש 10 ילדים שאוהבים רק גלידה ו- 10 ילדים שלא אוהבים גלידה וגם לא אוהבים שוקולד.